Dynamic Programming with Python dataclasses and joblib
Starting in Python 3.7, the module dataclasses introduces a decorator that allows us to create immutable structures (like tuples) but with their own batteries-included methods. I wanted to give dataclasses a try with some non-trivial workloads. Having always been interested the coin change problem where the solution involves dynamic programming, this seemed to be a good test of dataclasses.
Instead of the classic coin change problem (finding the minimum number of coins that add up to a given amount), however, here I want to keep track of all possible combinations. The end result (at the bottom of this post) is an interactive plot to explore the results.
Note: You can get the original Jupyter notebook for this post here.
from dataclasses import dataclass, field
from joblib import Memory
from bokeh.io import output_notebook, show
from bokeh.plotting import figure
output_notebook()
Here we'll use joblib to cache the results, so we don't need to redo computations we already have completed:
cachedir = "/tmp/memo1"
memory = Memory(cachedir, verbose=0)
memory.clear()
WARNING:root:[Memory(location=/tmp/memo1/joblib)]: Flushing completely the cache
Now, let's define the universe of possible coins.
# coins = [1, 2, 5, 10, 20, 50, 100] # European coins
# coins = [1, 5, 10, 25] # US Coins in wide circulation
coins = [1, 5, 10, 25, 50, 100] # All US Coins circulation
Here's where we create our dataclass—this will hold a specific collection of coins (the purse variable). We'll also define how to add coins from one purse to another (__add__) and set some helper methods allowing us to sort (__hash__), compare (__eq__, __le__, __lt__) and print (__repr__).
@dataclass
class change:
purse: list
value: int = field(init=False)
ncoins: int = field(init=False)
sort_index: int = field(init=False, repr=True)
def __post_init__(self):
self.value = sum(map(lambda x: x[0]*x[1], zip(coins, self.purse)))
self.ncoins = sum(self.purse)
self.sort_index = self.ncoins
def n(self, coin):
return self.purse[coins.index(coin)]
def __add__(self, other):
return change([x+y for x,y in zip(self.purse,other.purse)])
def __eq__(self, other):
return tuple(self.purse) == tuple(other.purse)
def __le__(self, other):
return self.ncoins <= other.ncoins
def __lt__(self, other):
return self.ncoins < other.ncoins
def __hash__(self):
return hash(tuple(self.purse))
def __repr__(self):
return f"({self.value}) {dict(zip(coins,self.purse))} {self.ncoins}"
Next we'll define the dynamic programming bit, which recursively looks for ways to make change, saving the results for a certain value, and reusing previously computed values.
empty_purse = [0]*len(coins)
@memory.cache
def get_change(val):
if val < coins[0]:
return [change(empty_purse)]
if val == coins[0]:
purse = empty_purse.copy()
purse[0] = 1
return [change(purse)]
final_list = []
for i, coin in enumerate(coins):
if val < coin:
continue
purse = empty_purse.copy()
purse[i] = 1
to_add = change(purse)
final_list += [prev + to_add for prev in get_change(val - coin)]
return list(set(final_list))
%time a = get_change(75)
CPU times: user 391 ms, sys: 74.3 ms, total: 466 ms
Wall time: 528 ms
That's pretty quick given all the possibilities (as we'll see). Let's compute all possibilities up to 100 cents.
max_n = 101
raw = [(x, sorted(get_change(x))) for x in range(1,max_n)]
points = []
uniques = []
min_coins = []
min_coins_scale = []
max_n = 0
for val, purse_list in raw:
ncoins = [x.ncoins for x in purse_list]
min_coins.append(min(ncoins))
min_coins_scale.append(min(ncoins)/val)
if val == 1:
uniques.append((val, len(ncoins)))
else:
if len(ncoins) != uniques[-1][1]:
uniques.append((val, len(ncoins)))
for nc in set(ncoins):
max_n = max(max_n, ncoins.count(nc))
combos = []
for x in [y for y in purse_list if y.ncoins == nc]:
combos.append("-".join([str(x) for x in x.purse]))
combos_str = "<br>".join(combos)
points.append((val, nc, ncoins.count(nc), combos_str))
print(max_n)
9
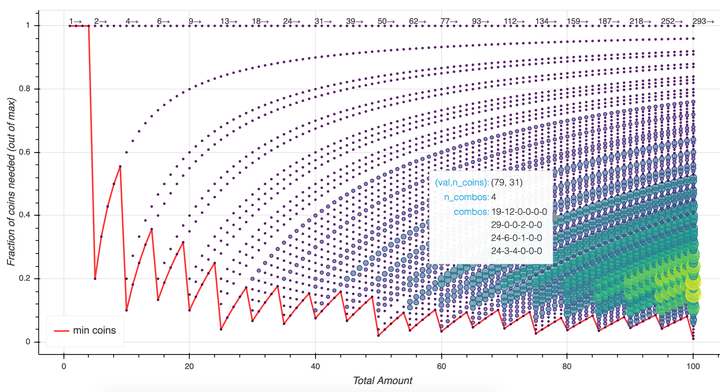
The value max_n is the most number of combinations for a certain fixed value size. For instance, if we want to make change for 97 cents with exactly 25 coins there are 7 different ways to do that:
| Penny | Nickel | Dime | Quarter |
|---|---|---|---|
| 17 | 0 | 8 | 0 |
| 22 | 0 | 0 | 3 |
| 17 | 6 | 0 | 2 |
| 12 | 12 | 0 | 1 |
| 12 | 9 | 4 | 0 |
| 7 | 18 | 0 | 0 |
| 17 | 3 | 4 | 1 |
Now let's make an interactive plot:
from bokeh.models import ColumnDataSource, LabelSet, Label
from bokeh.transform import linear_cmap
from bokeh.models import HoverTool
source = ColumnDataSource(data={
'x' : [x[0] for x in points],
'y' : [x[1]/(x[0]) for x in points],
'y_nat': [x[1] for x in points],
'n' : [max(2,20*x[2]/max_n) for x in points],
'n_nat': [x[2] for x in points],
'str': [x[3] for x in points]
})
hover = HoverTool(point_policy='snap_to_data', line_policy='nearest')
hover.tooltips = [
("(val,n_coins)", "(@x, @y_nat)"),
("n_combos", "@n_nat"),
("combos", "@str{safe}")
]
source_label = ColumnDataSource(data=dict(x=[x[0] for x in uniques],
y=[1 for x in uniques],
lab=[str(x[1]) + '→' for x in uniques]))
labels = LabelSet(x='x', y='y', text='lab', level='glyph',
x_offset=-1, y_offset=0.01, source=source_label, render_mode='canvas', text_font_size="8pt")
p = figure(plot_width=975, plot_height=500)
p.add_layout(labels)
p.xaxis.axis_label = 'Total Amount'
p.yaxis.axis_label = 'Fraction of coins needed (out of max)'
p.line([x[0] for x in raw], min_coins_scale, line_width=2, color="red", alpha=0.8, legend_label="min coins")
p.circle('x', 'y', size='n', color=linear_cmap('n', 'Viridis256', 2, 20),
fill_alpha=0.6, source=source)
p.legend.location = "bottom_left"
p.legend.click_policy="hide"
p.tools.append(hover)
show(p)
This should be a dynamic plot – you can zoom in to see some of the interesting structures. Hover over circles to see the coin combinations. I color coded and sized the circles so you can see where there is a lot of non-unique combinations. For example, we can see that 30 cents is the lowest value where there is a non-unique number of coin combinations (you can get 30 with 6 coins in 2 different ways). The numbers at the top of the plot show the total number of unique solutions. Try this out on your own; for example, what differences do you see with the Euro cent combination?